Reduction of the Occultation of bright star
5.3m HIP 22157 by Minor Planet 10734 Wieck
Friday, 8th February 2008, dusk, southwestern Germany
(Andreas Eberle)
![]()
This is a step by step guide about my reduction of the Wieck - Event,
recorded by H. Michels.
1. Digitalization:
The video tape was digitized and the target star (HIP 22157) and the (faint) comparison star (HD 287062) were evaluated (half-frame accuracy) using Limovie 0.9.28.
2. Comparison star:

Figure 1: comparison star
Although the comparison star was quite weak (and therefore noisy), there was
no indication for any dimming caused by atmospheric (clouds) effects (see figure
1). Therefore no adjustment was done.
3. Binary:

Figure 2: light curve
At first sight, the light curve (see figure 2) didn't show any significant
steps. From this "visual analysis" I concluded the following possibilities:
(a) There's no unknown close companion
(b) The companion is much weaker and has no significant influence on the data
(c) The two stars are very close (beyond my resolution) together
(d) The separation of the two stars is (close to) perpendicular to the asteroids
path
Since in step 4 we can see contact angles playing an important role, effects
from option (d) should be visible in the data.
4. Contact angles:
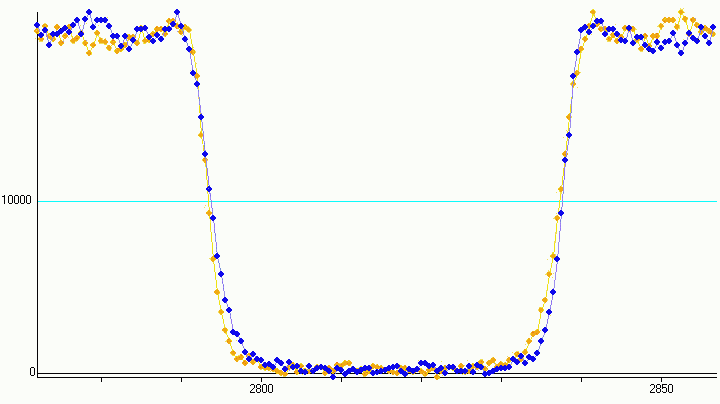
Figure 3: symmetry
The disappearance of the star takes longer than it's reappearance (see figure 3 to compare the original light curve (blue) with the mirrored (yellow) light curve). So contact angles seem to play an important role and must be beared in mind for the evaluation.
5. Telescope size:
The video was recorded using a 0.4m-Telescope. The asteroid traveled this distance in 0.00008 s, well beyond my resolution. Any effects here can therefore be ignored.
6. Star diameter:
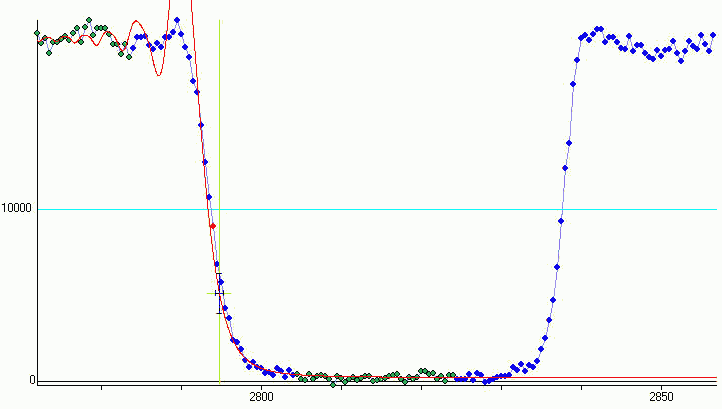
Figure 4: point source
The higher the "light density" of the star (= the smaller it's angular diameter), the more extensive the diffraction effects. In figure 4 you can see the theoretical light curve of a point source (angular diameter = 0, contact angle = 65°). Clearly visible are the overshoots at the beginning which are not supported by the data.
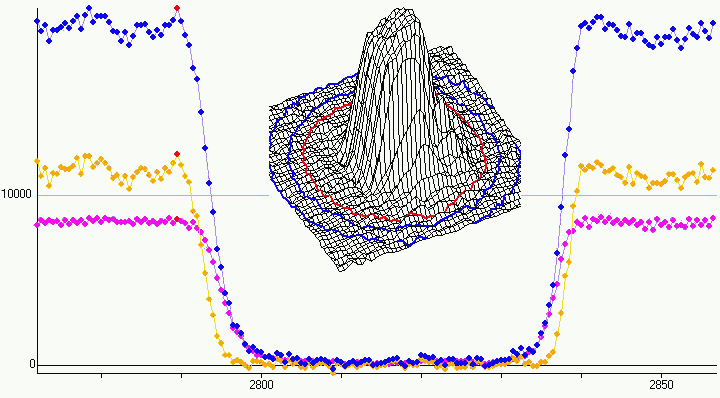
Figure 5: saturation
However, I feared I might miss some of this effect by saturated pixels in the center. To exclude this error source I measured an additional light curve of the center of the star (see figure 5, blue = original light curve, pink = center light curve, yellow = light curve without center). As can be seen, there are no saturation effects, moreover the 3D-star-image shows no signs of a flat, saturated center.
7. Video artifacts:
Although the analysis above showed no saturated pixels, another effect tampered with my data.
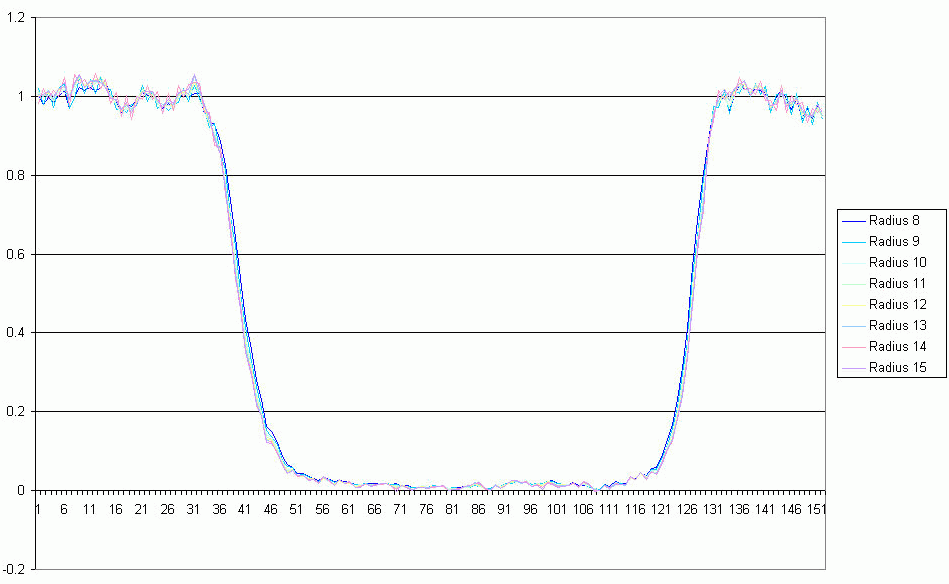
Figure 6: without reverse gamma correction
The pixel values are measured within a circle of certain radius. The bigger
this circle, the more background is visible. This leads to a drop in the
signal-to-noise ratio and therefore for more noisy data. But the whole event
also was shorter using a smaller radius (as can be seen in figure 6, the blue
"radius 8"-curve shows a shorter occultation as the wider radius 15 curve).
This is caused by the so-called "gamma correction" which alters the recording of
the linear information of the CCD towards a curve more comparable to the human
eye.
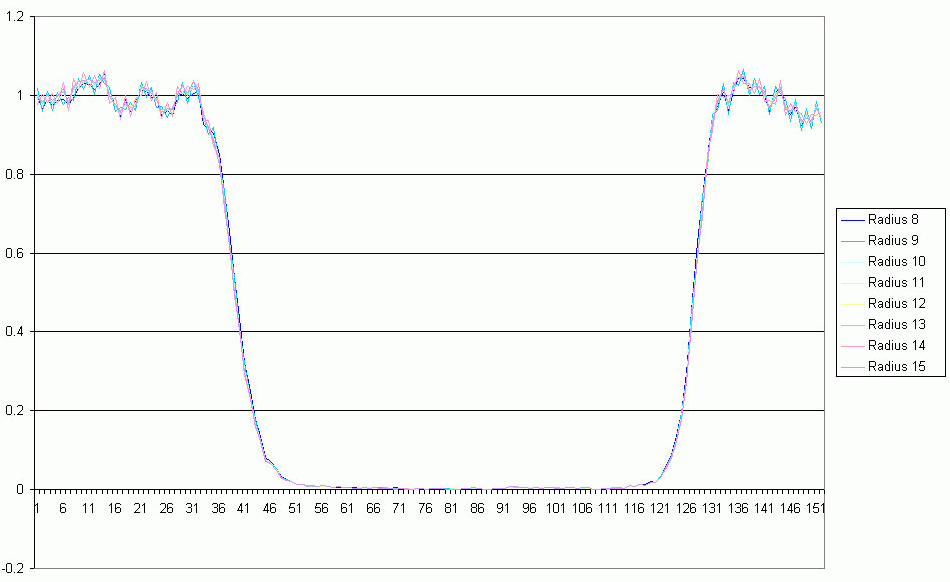
Figure 7: with reverse gamma correction
For measurements of light curves the data has to be linear. So the data was
calibrated using an inverse gamma correction (with a gamma of 0.45 according to
the data-sheet of the camera
http://www.lechner-cctv.de/download.php?FILE=Kameras_sk1004x.pdf ).
Figure 7 shows the same information with the recalibrated data.
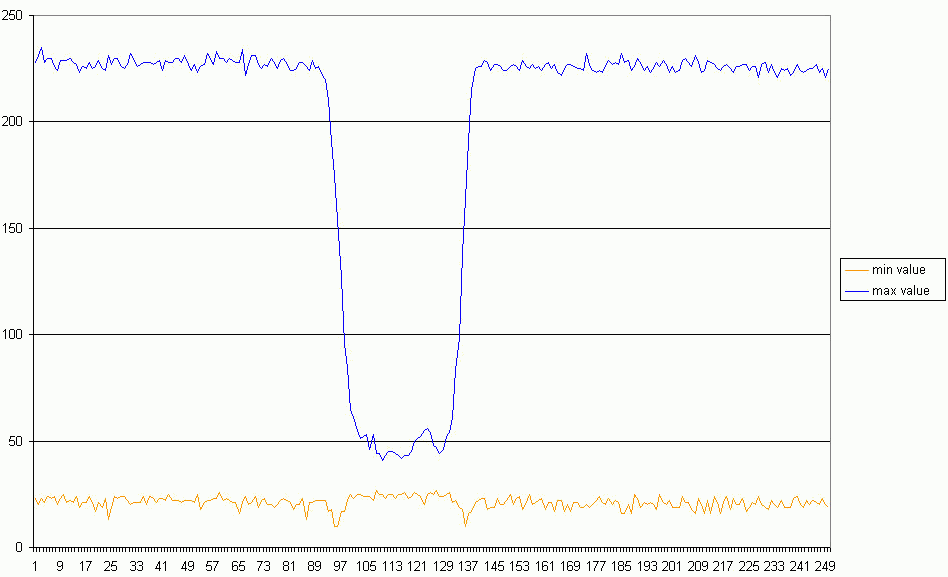
Figure 8: Min and Max-Values
Figure 8 shows two interesting things:
The orange curve of the minimal pixel value is slightly higher during the
occultation and shows in the beginning and end of the occultation significant
lower levels. These are probably common overshoot effects caused by contrast
enhancement (often you can see on videos around bright stars a very dark ring).
I do not believe, that this effect has a major impact on my evaluation and will
therefore be ignored.
The blue curve of the maximum pixel values shows a peak during the occultation
which is even visible in the video. This needs further investigation (see next
point).
8. Half-Flux-Diameter
Already during watching the video the peak of the maximum pixel value during
the occultation is visible. However, the full light curve doesn't show such
extreme irregularities (see figure 2).
To determine, if there is a real signal or not, I used the built-in
Half-Flux-Diameter measurement (http://www005.upp.so-net.ne.jp/k_miyash/occ02/halffluxdiameter/halffluxdiameter_en.html).
The Half-Flux-Diameter is comparable to FWHM-values, but easier to compute and
more stable in respect of noise.
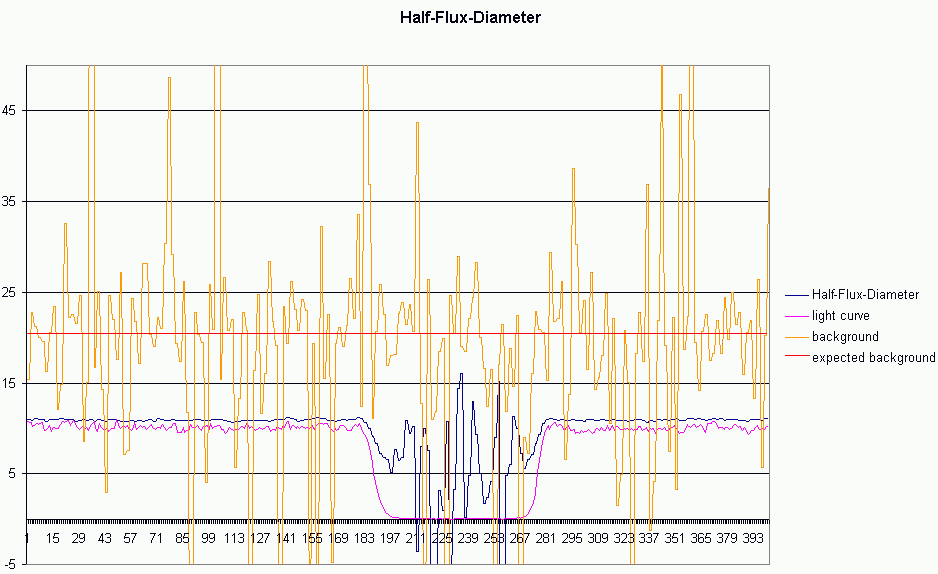
Figure 9: Half-Flux-Diameter
Figure 9 shows us the interesting result.
During the whole measurement the Half-Flux-Diameter differs from the expected
background signal (=no star). This means during the entire event a light source
is visible.
Therefore we have:
9. star diameter

Figure 10: star diameter
Figure 10 shows the residual sum-squared-error (calculated independently for disappearance and reappearance) for different star diameters (with optimal contact angle). The resulting light curves can be observed in figure 11 and 12.
.gif)
Figure 11: Disappearance (best fit)
.gif)
Figure 12: Reappearance (best fit)
Two problems are noticeable. First, the calculated star diameter may not
differ between dis- and reappearance (0.50mas vs. 0.40mas).
Second, the expected diameter of the A2m star is d = 2.5 +/- 0.5 solar diameters
which would result (in 82 +/- 6 parsec distance) in a star
diameter between 0.21 mas and 0.37 mas, meaning that at least the 0.50mas from
disappearance is considerably too high.
10. after all a double star?
Jean Lecacheux pointed out to me, that most A2m stars are close binaries. Having some effects that could be considered as a hidden companion, I reworked my data.
.gif)
Figure 13: Double star, disappearance (best fit)
Figure 13 shows such a possible binary. We have to keep two things in mind. First, Limovie can't calculate binaries with different diameters (both binaries are here considered to have 0.37mas). Second and much more grave - to be honest - the position of the first occulted star is nonsense. Limovie uses the additional degrees of freedom to interpolate the noise at the beginning, there is no real data supporting it's position.

Figure 14: Double star, reappearance
Figure 14 shows, that a binary (with 0.37mas) doesn't contradict the
reappearance values.
Is there still something to be learned?
Yes, we see that
Disappearance:
single: Frame 2794.0 -5ms +/-2ms, contact angle 43.6°
double: Frame 2794.0 +8ms +/-1ms, contact angle 53.8°
Reappearance:
single: Frame 2837.5 -5ms +/-2ms, contact angle 34.1°
double: Frame 2837.5 -3ms +/-1ms, contact angle 37.5°
Although we can't tell if and where there is a companion star, we can use the calculated data for determining the asteroids size.
11. Conclusion
Final Results:
Assuming an ellipsoid, these data lead to the conclusion, that the asteroid is about 13.6 km x 10.5 km in Diameter (see figure 15).
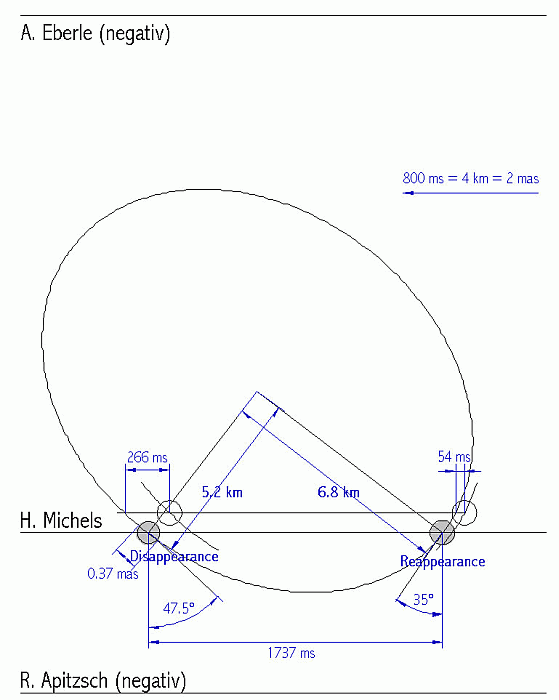
Figure 15: Final result
In figure 15 the position of the above calculated possible companion star is included. Although there are some clues leading to the conclusion, that the target star is a close binary, the position of the companion was only for demonstration purposes included - the data are by far to noisy to really measure it's position.
Please feel free to let me know your comments about this analysis,
Andreas Eberle
![]()
Please have a look to Eric Frappa's observers archive about this event.
Special thanks to Andrey Plekhanov and Steve Preston for providing us with excellent predictions and to all observers spinning such a fine 'observation grid' that we sucessfully caught Wieck in our net !
Last update: 04/26/08 15:29 +0200